第3章 微分
Tip
上一章我们通过极限给出了导数的定义, 并指出导数的几何意义是函数某一点处切线的斜率. 通过计算函数切线的斜率, 我们可以判断函数的增减性及其极值.
本章我们将介绍微分的概念, 并揭示微分与导数之间的朴实却深刻的联系. 微分是微积分的核心思想, 将在后续的课程中贯穿始终.
3.1 微分的概念
Tip
微分 (differential) 的意思是 无穷小的改变量 (infinitesimally small change),莱布尼茨为微分创立了其专属符号 "", 例如 表示变量 的微分, 表示变量 的微分. 与之对应的, 物理上经常用 表示一个很小的改变量,比如一小段位移. 直观上看, 和 想传达的意思很相近, 都是很小的量, 但是在数学它们是有区别的.
Note
如图, 考虑一个做直线运动的物体, 它在经过一小段时间 之后位移的变化量为 . 此时我们考虑 的极限, 就得到时间的微分 以及对应的位移的微分 .
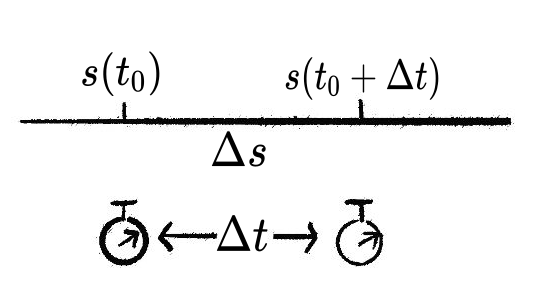
Note
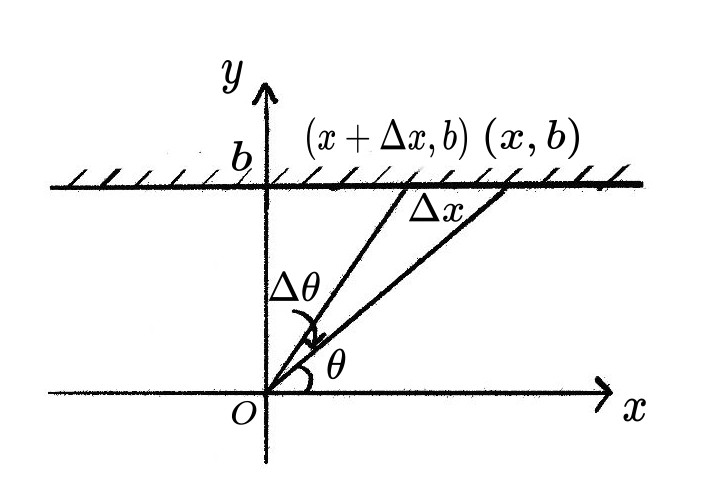
如图, 从原点位置以角度 发射一束激光, 设激光与直线 的交点坐标为 . 如果我们将发射角做一个微小的改变 , 与之对应的激光光斑的位置会在 -轴方向上发生了一个 的偏移. 此时我们考虑 的极限, 就得到角度的微分 以及对应的x的微分 .
3.1.1 微分与导数
Tip
在研究实际问题的时候, 我们经常关心两个微分之间的关系. 例如, 设想我们需要控制一个机械手臂在黑板上画图, 粉笔移动一个小位移, 机械臂的各个关节也要相应的移动一个小量. 我们可以把关节移动的小量认为是 , 粉笔移动的小量认为是 . 很多时候我们关心两个微分之间的联动关系, 比如在机器人控制领域, 给定 计算 叫做正动力学, 给定 计算 叫做逆动力学. 又比如在例1中 与 的关系反映了物体的位移随时间的变化关系; 例2中 与 的关系反映了激光光斑的位置随发射角度之间的变化关系, 这些都是物理中所关心的量.
那么如何确定两个微分之间的关系呢? 如果我们能够写出两个变量之间所满足的函数关系, 很容易就可以得到这两个变量所对应的微分之间的关系, 这是微分学的一个重要成就.
Important
微分与导数的关系
一般的, 假定两个变量 , 满足函数关系 , 则 .
Note
我们首先通过数值计算来验证上述关系.
例1: 我们分别考虑两种直线运动: 匀速运动** 和 匀加速运动.**
对于匀速运动,
根据微分公式, 位移的微分与时间的微分满足关系:
对于初速度为0的匀加速运动, 其位移随时间的函数为
根据微分公式, 位移的微分与时间的微分满足关系:
下表给出了 取不同数值时所对应得 的真实值和微分公式的预测值 ( ).
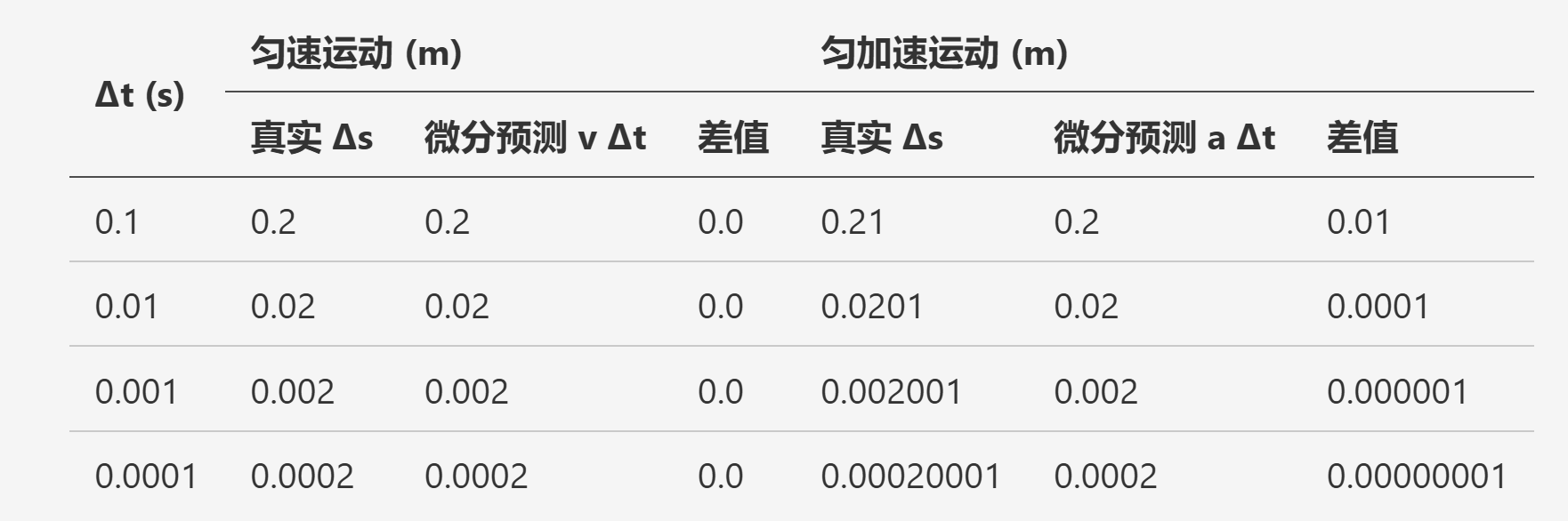
从表中可以看到, 对于匀速运动, 所有情况下差值均为 0, 这表明对于线性函数,微分给出的是精确的, 但这仅限于线性函数的特例. 对于更加一般的匀加速运动, 差值不等于0, 但会随着 的减小而迅速减小. 这一观察提示我们, 当 时, 误差的极限也区域0, 由此得到微分公式中的等式成立.
Note
例2: 在这个例子中, 与 的函数关系为
根据微分公式, 我们有
也就是说, 激光出射角度每增加 , 光斑就会左移(负号) .
我们再稍微拓展一下, 如果我们关心的不是横坐标 , 而是激光飞行的距离 , 则
此时的微分公式给出
也就是说, 激光出射角度每增加 , 激光得飞行距离就会缩短(负号) .
下表给出了取不同的 时 和 的真实变化量和微分公式预测的变化量的对比( ):
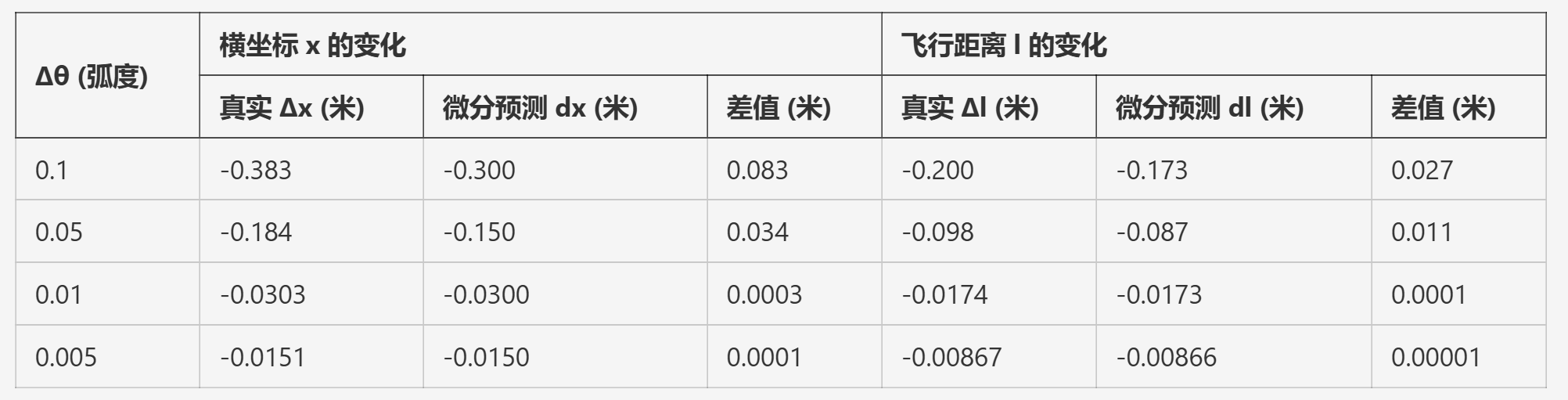
从表中可以看出, 随着 的减小, 微分公式与精确值的误差也迅速减小, 提示当 时, 误差的极限也区域0.
综合上面的例子可以得到如下结论: 当 很小时, 近似满足
而取 的极限, 上式约等于变成等于
Warning
接下来我们结合导数的定义来理解微分公式. 在上一章中,我们曾从函数图像切线的角度出发,借助极限给出导数的定义:
上式的分子就是 . 因此形式上我们有
由此可见,当 时,差分商 的极限正是微分之商 。
在微积分的逻辑体系内, 最初是一个整体符号代表导数。事实上,我们也常用符号 表示导数,常见的表达方式包括:
但这里我们形式上将 和 作为独立的“微分”概念,从而将导数的定义式
变形成等式
Important
微分公式表明函数值 的微分与自变量 的微分呈线性关系,它的背后体现了化曲为直的思想, 具体体现在
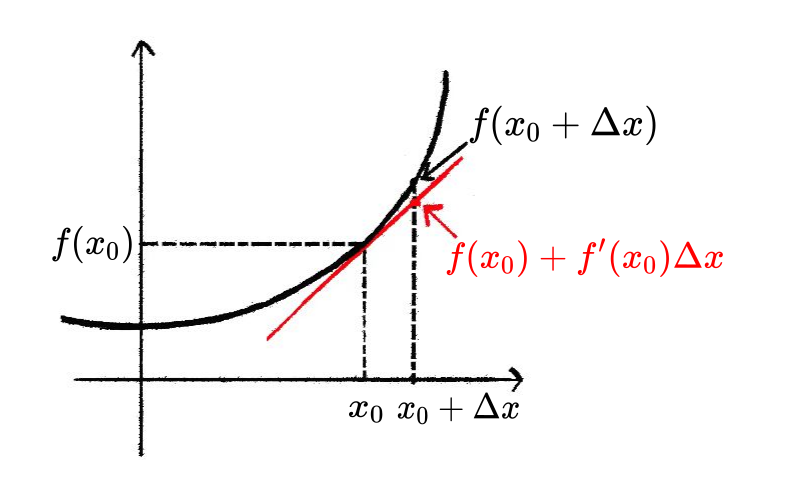
最后一个公式说明,函数在 附近可近似看作一条过点 、斜率为 的直线. 在局部用一条直线来近似函数也就是所谓的化曲为直, 这是微积分中一个极其重要的思想.
Warning
基于微分符号所建立的导数定义与运算规则非常直观,在后续课程中,我们将进一步领略微分思想的强大力量,并体会良好符号系统为数学带来的美感与实用价值。
3.2 借助微分计算导数
Tip
借助微分的思想和符号可以帮助我们去处理更加复杂的求导运算, 包括复合函数求导和隐函数求导.
3.2.1 复合函数求导的链式法则
Important
链式法则 (Chain Rule)
若函数 在点 可导,且 在点 可导,则:
基于微分的思想, 链式法则可以直观的理解为: 分子分母同时乘以无穷小量 , 得到
Note
P90 例9: 设函数 ,求
解:
可看作由 , 复合而成,因此:
Note
P90 例10: 设函数 ,求
解:
可看作由 复合而成。因
所以
Note
P91 例11: 设 ,求 .
解: 可看作由 , 复合而成。所以
Note
P92 例12: 设 ,求 .
解 : 可看作由 , 复合而成。
所以
Note
P92 例13: 设 ,求
解: 所给函数可分解为 。
Note
P92 例14: 设 ,求
解:
逐层求导:
根据链式法则:
Note
P93 例15: 设 ,求
解 :
3.2.2 隐函数求导
Tip
隐函数将自变量 和函数值 通过某个等式联系起来, 从这个等式里我们可以推测 和 之间的关系, 一些复杂的函数的导数通过隐函数更容易计算.
Note
P101 例1: 求由方程 所确定的隐函数的导数 .
解 : 将方程两边对 求导,注意 是 的函数:
左边求导:
右边求导:
令两边相等:
合并关于 的项:
解得:
即 .
Note
P102 例2: 求由方程 所确定的隐函数在 处的导数 .
解 :
将方程两边对 求导(注意 是 的函数):
解关于 的方程:
解得
求 时的 值:
解得实数解为
计算 处的导数值:
将 , 代入导数表达式:
Note
P102 例3: 求双曲线 在点 处的切线方程.
解 : 对双曲线方程两边关于 求导:
解得
计算切点处斜率,在点 处:
于是所求的切线方程为:
3.2.3 反函数求导
Note
[不要用书上的做法, 用隐函数求导]
P88 例6: 设 (),用隐函数求导法求
解 : 由 可得直接函数关系: ,
对 两边关于 求导(注意 是 的函数):
将 用表示:
利用三角恒等式:
(当 时,,故取正根)
故得到结果:
用类似的方法可得反余弦函数的导数公式
.
Note
[不要用书上的做法, 用隐函数求导]
P88 例7: 设 (),用隐函数求导法求
解 :
由 可得直接函数关系: ,
对 两边关于 求导(注意 是 的函数):
将 用 表示:
利用三角恒等式:
故得到结果:
用类似的方法可得反余切函数的导数公式 .
Note
P103 例5: 求 ()的导数
解 : 利用对数求导法
两边取对数:
两边对 求导得:
解出 得到:
Note
P103 例6: 求 的导数
解 : 假设 ,在等式两边取对数:
对两边关于 求导(注意 是 的函数):
整理得到导数表达式:
将 代入,得:
3.2.4 更多的高阶导数计算
Tip
微分的思想也可以帮助我们来理解和计算高阶导数, 结合链式法则, 我们可以进行更加复杂的计算.
Caution
常用记号
, , , , .
, , , , .
Note
P97 例2: 设 ,求
解 : 求一阶导数 ,
求二阶导数 :
最终得到:
Note
P97 例4: 求指数函数 ( 为常数)的 阶导数
解 :
一阶导数:
二阶导数:
三阶导数:
四阶导数:
观察规律可知,每求导一次会多乘一个系数 ,因此一般形式为:
Note
P103 例4: 求由方程 所确定的隐函数的二阶导数 .
解 : 对原方程两边关于 求导:
对一阶导数 两边关于 求导:
代入 得到:
Note
最后我们回过头来看一下图2中所给出的例子. 上面我们已经得到
如果我们希望计算 与 的关系,即 ,可以采用以下两种方法:
方法一: 建立 x 与 l 的显式函数关系
由 可得 ,代入 得:
对 求导得:
因此 。
方法二: 直接利用微分之比
由 和 的表达式直接相除:
同样得到 。
两种方法结果一致,但第二种方法通过直接操作微分,避免了复杂的函数关系和求导过程,显示了微分运算的简洁性与灵活性。在实际问题中,灵活运用微分关系可以大大简化计算,这正是微分思想的强大之处。
3.3 借助微分计算极限
Tip
借助微分的思想和符号还可以帮助我们去理解一个较为使用的求极限方法: 洛必达法则.
3.3.1 洛必达法则
Important
洛必达法则是用于计算在不定形式 (未定式, 即: 或) 下极限的有力工具.
如果函数 和 在点 的某个邻域内可导,且在该点附近有:
那么
前提是后者的极限存在.
注意: 有时可能需要多次应用洛必达法则, 特别是当 仍然是 或 的形式时.
Warning
下面我们借助微分的思想来理解洛必达法则.
当 充分接近 时,我们可以用函数的线性近似(即微分)来替代原函数。由于 ,在点 附近有:
因此,原比式的极限可近似表示为:
当 时,这一近似将趋于精确。这正是洛必达法则的直观含义——在极限过程中,分子与分母的变化趋势由它们在该点的导数之比决定。
对于 型未定式,虽然不能直接使用上述推导,但微分思想仍然适用: 此时我们比较的是 与 在 过程中的相对变化速率,而导数正是刻画这种瞬时变化率的工具。
需要强调的是,上述推导仅为理解洛必达法则提供了直观的几何图像。严格证明需依赖柯西中值定理,该定理能够将 替换成 ,其中 位于 与 之间, 从而得到使用起来更加灵活的洛必达法则。这部分内容我们放在了后面的章节中.
Note
P134 例1: 求 ()
解 :
Note
P134 例2: 求
解 :
注意,上式中的 已不是未定式,不能对它应用洛必达法则,否则要导致错误结果。以后使用洛必达法则时应当经常注意这一点,如果不是未定式,那么就不能应用洛必达法则。
Note
P134 例3: 求
解 :
Note
P134 例4: 求
解 :
Note
P135 例5: 求
解 :
Note
P135 例6: 求 为正整数
解 : 相继应用洛必达法则 次,得
事实上,如果例6中的 不是正整数而是任何正数,那么极限仍为零。
对数函数 、幂函数 、指数函数 均为当 时的无穷大,但从例5、例6可以看出,这三个函数增大的"速度"是很不一样的,幂函数增大的"速度"比对数函数快得多,而指数函数增大的"速度"又比幂函数快得多。
下表列出了 分别取 10, 100, 1000 时,函数 , , 及 相应的函数值。从中可以看出当 增大时这几个函数增大"速度"快慢的情况。
Note
P135 例7: 求
解 :
当 时,上式右端是未定式 ,应用洛必达法则,得
Note
P136 例8: 求
解 : 这是未定式 。因为
当 时,上式右端是未定式 ,应用洛必达法则,得
Note
P136 例9: 求
解 : 这是未定式 . 设 ,取对数得
当 时,上式右端是未定式 。应用例7的结果,得
因为 ,而 (当),所以
Note
P136 例10: 求
解 : 如果直接用洛必达法则,那么分母的导数(尤其是高阶导数)较繁。如果作一个等价无穷小替代,那么运算就方便得多。其运算如下:
Warning
后面的章节中, 我们会介绍更加强大的计算极限的工具---泰勒展开. 而泰勒展开体现的也是微分的思想.